LeetCode 솔루션

1584. Min Cost to Connect All Points

mingki 쪽지보내기 메일보내기 자기소개 아이디로 검색 전체게시물 작성
작성일 2022.04.25 22:22

7,272 조회
1 댓글
0 추천
0 비추천
목록

글검색

게시글 쓰기

[LeetCode 시즌 3] 2022년 4월 25일 문제입니다

https://leetcode.com/problems/min-cost-to-connect-all-points/

[Medium] 1584. Min Cost to Connect All Points

You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].

Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.

Example 1:

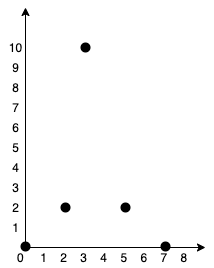
Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
Output: 20
Explanation: 

We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.

Example 2:

Input: points = [[3,12],[-2,5],[-4,1]]
Output: 18

Constraints:

1 <= points.length <= 1000
-106 <= xi, yi <= 106
All pairs (xi, yi) are distinct.

#LeetCode, #Amazon, #Array, #Union Find, #Minimum Spanning Tree(MST)

링크

https://leetcode.com/problems/min-cost-to-connect-all-points/ 2449 회 연결

익명
작성일 2022.04.29 11:23

class Solution:
    def minCostConnectPoints(self, points: List[List[int]]) -> int:
        hpq = []
        parent = defaultdict(int)
        self.ans = 0
        
        def find(x, parent):
            if parent[x] == x:
                return x
            parent[x] = find(parent[x], parent)
            return parent[x]
        
        def union(x, y, parent, temp):
            px = find(x, parent)
            py = find(y, parent)
            if px != py:
                parent[px] = py
                return temp
            return 0
        
        for i in range(len(points)):
            parent[(points[i][0], points[i][1])] = (points[i][0], points[i][1])
            for j in range(i + 1, len(points)):
                temp = abs(points[i][0] - points[j][0]) + abs(points[i][1] - points[j][1])
                hpq.append([temp, i, j])
        hpq.sort()
        for i in range(len(hpq)):
            p = hpq[i]
            self.ans += union(tuple(points[p[1]]), tuple(points[p[2]]), parent, p[0])
        return self.ans

Runtime: 7351 ms, faster than 5.00% of Python3 online submissions for Min Cost to Connect All Points.
Memory Usage: 97.8 MB, less than 31.36% of Python3 online submissions for Min Cost to Connect All Points.
[code=python]class Solution:
    def minCostConnectPoints(self, points: List[List[int]]) -> int:
        hpq = []
        parent = defaultdict(int)
        self.ans = 0
        
        def find(x, parent):
            if parent[x] == x:
                return x
            parent[x] = find(parent[x], parent)
            return parent[x]
        
        def union(x, y, parent, temp):
            px = find(x, parent)
            py = find(y, parent)
            if px != py:
                parent[px] = py
                return temp
            return 0
        
        for i in range(len(points)):
            parent[(points[i][0], points[i][1])] = (points[i][0], points[i][1])
            for j in range(i + 1, len(points)):
                temp = abs(points[i][0] - points[j][0]) + abs(points[i][1] - points[j][1])
                hpq.append([temp, i, j])
        hpq.sort()
        for i in range(len(hpq)):
            p = hpq[i]
            self.ans += union(tuple(points[p[1]]), tuple(points[p[2]]), parent, p[0])
        return self.ans
            
            
        [/code]