LeetCode 솔루션

700. Search in a Binary Search Tree

mingki 쪽지보내기 메일보내기 자기소개 아이디로 검색 전체게시물 작성
작성일 2022.04.13 19:24

7,316 조회
3 댓글
0 추천
0 비추천
목록

글검색

게시글 쓰기

[ Leetcode 시즌 3 ] 2022년도 4월 13일 문제 입니다.

[Easy] 700. Search in a Binary Search Tree

You are given the root of a binary search tree (BST) and an integer val.

Find the node in the BST that the node's value equals val and return the subtree rooted with that node. If such a node does not exist, return null.

Example 1:

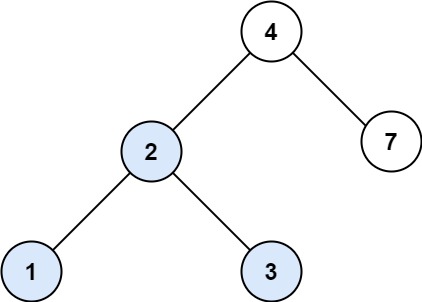
Input: root = [4,2,7,1,3], val = 2
Output: [2,1,3]

Example 2:

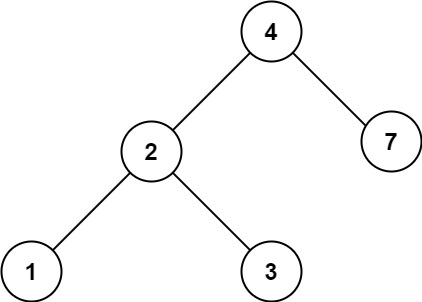
Input: root = [4,2,7,1,3], val = 5
Output: []

Constraints:

The number of nodes in the tree is in the range [1, 5000].
1 <= Node.val <= 107
root is a binary search tree.
1 <= val <= 107

#leetcode, #문제풀이, #시즌3, #easy, #Microsoft, #Amazon, #Tree, #Binary Search Tree, #Binary Tree

링크

https://leetcode.com/problems/search-in-a-binary-search-tree/ 2338 회 연결

익명
작성일 2022.04.13 20:10

C++
Runtime: 60 ms, faster than 39.28% of C++ online submissions for Search in a Binary Search Tree.
Memory Usage: 34.8 MB, less than 66.88% of C++ online submissions for Search in a Binary Search Tree.

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        for (; root && root->val != val; root = val < root->val ? root->left : root->right)
            ;
        return root;
    }
};

익명
작성일 2022.04.14 10:35

재귀적 접근, node가 null이거나 val을 못찾으면 null값 return.
현재 노드의 val이 target val보다 작으면, root의 왼쪽 방향으로 탐색
현재 노드의 val이 target val보다 크면, root의 오른쪽 방향으로 탐색

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {     
        if(root == null || val == root.val){
            return root;
        }
        return val < root.val ? searchBST(root.left, val) : searchBST(root.right, val);
        
    }
}

익명
작성일 2022.04.14 21:48

Intuition
Binary Search Tree:
each node > left nodes
each node < right nodes
https://www.youtube.com/watch?v=Lr2oxJlnLMM

Approach 1: Recursion
TC: O(H) where H is a tree height.
SC: O(H) to keep the recursion stack

Approach 2: Iteration
TC: O(H)
SC: O(1)

class Solution:
    def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:   
        if root is None or val == root.val:
            return root
        
        if val < root.val:
            return self.searchBST(root.left, val)
        
        else:
            return self.searchBST(root.right, val)

class Solution:
    def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
        cur = root
        
        while cur and cur.val != val:
            
            if val < cur.val:
                cur = cur.left
            else:
                cur = cur.right
        
        
        return cur