LeetCode 솔루션 분류
[12/13] 931. Minimum Falling Path Sum
본문
931. Minimum Falling Path Sum
Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.
A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).
Example 1:
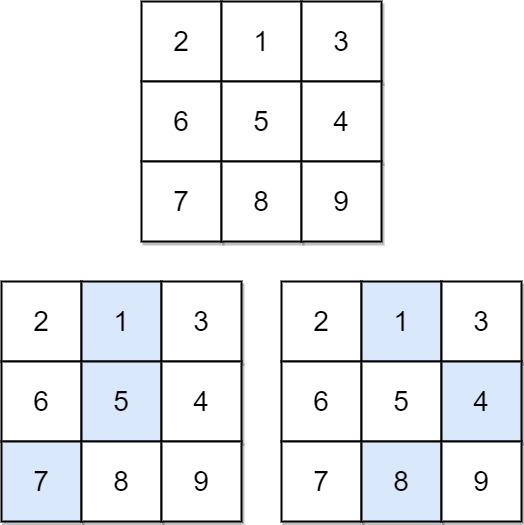
Input: matrix = [[2,1,3],[6,5,4],[7,8,9]] Output: 13 Explanation: There are two falling paths with a minimum sum as shown.
Example 2:
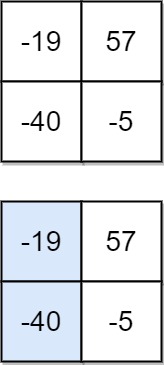
Input: matrix = [[-19,57],[-40,-5]] Output: -59 Explanation: The falling path with a minimum sum is shown.
Constraints:
n == matrix.length == matrix[i].length1 <= n <= 100-100 <= matrix[i][j] <= 100
Accepted
215.7K
Submissions
311.7K
Acceptance Rate
<span class="text-md font-medium" style="border: 0px solid; box-sizing: border-box; --tw-border-spacing-x:0; --tw-border-spacing-y:0; --tw-translate-x:0; --tw-translate-y:0; --tw-rotate:0; --tw-skew-x:0; --tw-skew-y:0; --tw-scale-x:1; --tw-scale-y:1; --tw-pan-x: ; --tw-pan-y: ; --tw-pinch-zoom: ; --tw-scroll-snap-strictness:proximity; --tw-ordinal: ; --tw-slashed-zero: ; --tw-numeric-figure: ; --tw-numeric-spacing: ; --tw-numeric-fraction: ; --tw-ring-inset: ; --tw-ring-offset-width:0px; --tw-ring-offset-color:#fff; --tw-ring-color:rgba(59,130,246,0.5); --tw-ring-offset-shadow:0 0 #0000; --tw-ring-shadow:0 0 #0000; --tw-shadow:0 0 #0000; --tw-shadow-colored:0 0 #0000; --tw-blur: ; --tw-brightness: ; --tw-contrast: ; --tw-grayscale: ;
관련자료
-
링크
댓글 1
학부유학생님의 댓글
- 익명
- 작성일
class Solution:
def minFallingPathSum(self, matrix: List[List[int]]) -> int:
dic = {}
ROW, COL = len(matrix), len(matrix[0])
directions = [(1,-1),(1,1),(1,0)]
def dfs(r, c):
if r == ROW-1:
return matrix[r][c]
if (r,c) in dic: return dic[(r,c)]
min_path = float('inf')
for rd, cd in directions:
nr, nc = r + rd, c+cd
if 0<=nr<ROW and 0<=nc<COL:
min_path = min(min_path, dfs(nr,nc))
dic[(r,c)] = min_path + matrix[r][c]
return min_path + matrix[r][c]
return min(dfs(0,c) for c in range(COL))









