LeetCode 솔루션

1631. Path With Minimum Effort

mingki 쪽지보내기 메일보내기 자기소개 아이디로 검색 전체게시물 작성
작성일 2022.04.27 21:47

7,368 조회
1 댓글
0 추천
0 비추천
목록 게시글 쓰기

[LeetCode 시즌 3] 2022년 4월 27일 문제입니다.

https://leetcode.com/problems/path-with-minimum-effort/

[Medium] 1631. Path With Minimum Effort

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

Example 1:

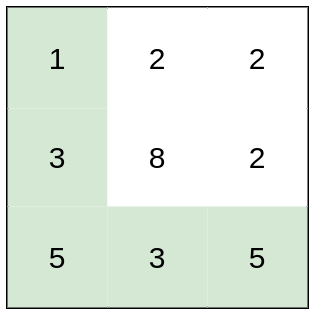
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

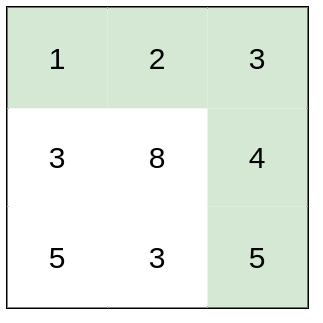
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

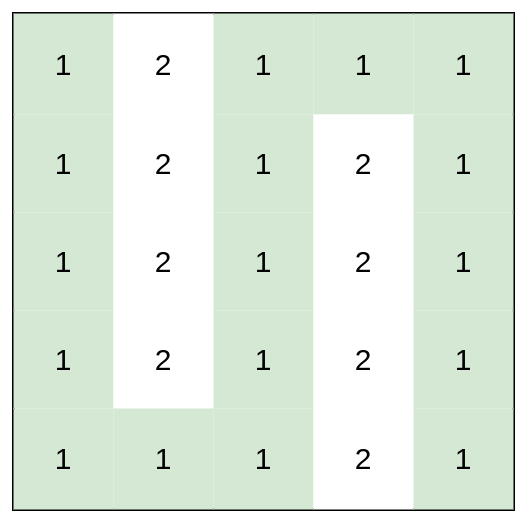
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

Constraints:

rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 106

#LeetCode, #Google, #Array, #Binary Search, #Depth-First Search(DFS), #Breadth-First Search(BFS), #Union Find, #Heap, #Priority Queue, #Matrix

링크

https://leetcode.com/problems/path-with-minimum-effort/ 2810 회 연결

익명
작성일 2022.04.27 23:04

class Solution {
public:
    int minimumEffortPath(vector<vector<int>>& heights) {
        typedef tuple<int, int, int> pos; // cost, y, x
        priority_queue<pos, vector<pos>, greater<pos>> q;
        const size_t h = heights.size(), w = heights[0].size();
        vector<vector<bool>> v(h, vector<bool>(w));
        q.emplace(0, 0, 0);
        while(!q.empty()) {
            auto[cost, y ,x] = q.top();
            if (y == h-1 && x == w-1) return cost;
            q.pop();
            if (v[y][x]) continue;
            v[y][x] = true;
            for(auto [dy, dx] : vector<pair<int, int>>{{1,0}, {-1,0}, {0,1}, {0,-1}}) {
                auto [ny, nx] = tuple(y + dy, x + dx);
                if (ny < 0 || nx < 0 || ny == h || nx == w || v[ny][nx]) continue;
                q.emplace(max(cost, abs(heights[ny][nx] - heights[y][x])), ny, nx);
            }
        }
        return -1;
    }
};

C++ Dijkstra solution
Runtime: 204 ms, faster than 77.24% of C++ online submissions for Path With Minimum Effort.
Memory Usage: 31 MB, less than 51.34% of C++ online submissions for Path With Minimum Effort.
[code=C++]class Solution {
public:
    int minimumEffortPath(vector<vector<int>>& heights) {
        typedef tuple<int, int, int> pos; // cost, y, x
        priority_queue<pos, vector<pos>, greater<pos>> q;
        const size_t h = heights.size(), w = heights[0].size();
        vector<vector<bool>> v(h, vector<bool>(w));
        q.emplace(0, 0, 0);
        while(!q.empty()) {
            auto[cost, y ,x] = q.top();
            if (y == h-1 && x == w-1) return cost;
            q.pop();
            if (v[y][x]) continue;
            v[y][x] = true;
            for(auto [dy, dx] : vector<pair<int, int>>{{1,0}, {-1,0}, {0,1}, {0,-1}}) {
                auto [ny, nx] = tuple(y + dy, x + dx);
                if (ny < 0 || nx < 0 || ny == h || nx == w || v[ny][nx]) continue;
                q.emplace(max(cost, abs(heights[ny][nx] - heights[y][x])), ny, nx);
            }
        }
        return -1;
    }
};[/code]