LeetCode 솔루션

[9/14] 1457. Pseudo-Palindromic Paths in a Binary Tree

학부유학생 쪽지보내기 메일보내기 자기소개 아이디로 검색 전체게시물 작성
작성일 2022.09.14 08:18

6,404 조회
1 댓글
0 추천
0 비추천
목록 게시글 쓰기

1457. Pseudo-Palindromic Paths in a Binary Tree

Medium

187662Add to ListShare

Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.

Return the number of pseudo-palindromic paths going from the root node to leaf nodes.

Example 1:

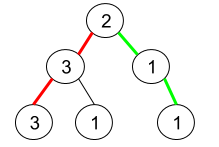
Input: root = [2,3,1,3,1,null,1]
Output: 2 
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 2:

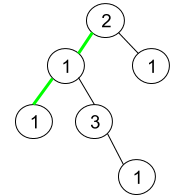
Input: root = [2,1,1,1,3,null,null,null,null,null,1]
Output: 1 
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 3:

Input: root = [9]
Output: 1

Constraints:

The number of nodes in the tree is in the range [1, 105].
1 <= Node.val <= 9

Accepted

88,348

Submissions

129,778

#Bloomberg, #Amazon

링크

https://leetcode.com/problems/pseudo-palindromic-paths-in-a-binary-tree/ 833 회 연결

익명
작성일 2022.09.14 08:19

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
from collections import Counter
class Solution:
    def pseudoPalindromicPaths (self, root: Optional[TreeNode]) -> int:
        # set elements == 0: all even 
        # set elements == 1: all even except one
        # set elements >=2 : cannot be palindrome
        
        elements = set()
        
        def dfs(node):
            if not node: return 0
            
            # modify set
            if node.val not in elements: elements.add(node.val)
            else: elements.remove(node.val)
                
            if not node.left and not node.right:
                return_val = 1 if len(elements)<=1 else 0
            else:
                return_val = dfs(node.left) + dfs(node.right)
            
            # UNDO the modification from the above for other dfs
            if node.val not in elements: elements.add(node.val)
            else: elements.remove(node.val)
            
            return return_val
            
        
        return dfs(root)

Runtime: 1255 ms, faster than 66.67% of Python3 online submissions for Pseudo-Palindromic Paths in a Binary Tree.
Memory Usage: 84.7 MB, less than 86.60% of Python3 online submissions for Pseudo-Palindromic Paths in a Binary Tree.
[code=Python 3]# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
from collections import Counter
class Solution:
    def pseudoPalindromicPaths (self, root: Optional[TreeNode]) -> int:
        # set elements == 0: all even 
        # set elements == 1: all even except one
        # set elements >=2 : cannot be palindrome
        
        elements = set()
        
        def dfs(node):
            if not node: return 0
            
            # modify set
            if node.val not in elements: elements.add(node.val)
            else: elements.remove(node.val)
                
            if not node.left and not node.right:
                return_val = 1 if len(elements)<=1 else 0
            else:
                return_val = dfs(node.left) + dfs(node.right)
            
            # UNDO the modification from the above for other dfs
            if node.val not in elements: elements.add(node.val)
            else: elements.remove(node.val)
            
            return return_val
            
        
        return dfs(root)[/code]